已知P是椭圆x2/4+y2=1上的一点，F1、F2是椭圆的两
已知P是椭圆x2/4+y2=1上的一点，F1、F2是椭圆的两个焦点，.
已知P是椭圆x2/4+y2=1上的一点，F1、F2是椭圆的两个焦点，且
F1PF2=60°，求△F1PF2的面积
正确答案： 令|PF1|=x，|PF2|=y
cos60=1/2=(x2+y2-4c2)/2xy => xy=(x+y)2-2xy-12
椭圆性质，x+y=2a=4
xy=4/3
S=0.5*xy*sin60=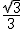
源于查字典网
正确答案： 令|PF1|=x，|PF2|=y
cos60=1/2=(x2+y2-4c2)/2xy => xy=(x+y)2-2xy-12
椭圆性质，x+y=2a=4
xy=4/3
S=0.5*xy*sin60=
